Geolocation

FAQ: Location Precision for Zmanim Calculations

While overly broad ZIP code based zmanim geolocation can be an issue in calculating zmanim accurately, going overboard in geolocation precision and accuracy for zmanim is a (harmless) waste of time.
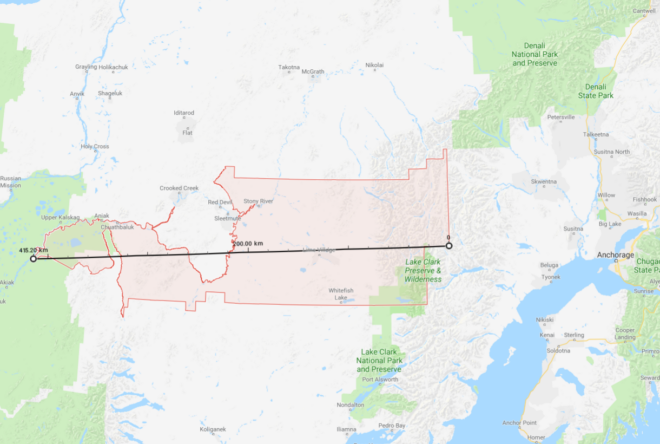
Let’s start with the basics. Asking what the zmanim are for the USA is too broad of a location. Narrowing it down to a state is also too broad since zmanim at one side of the state are likely to be different than the other side. How small (or precise) does an area have to be for the zmanim calculated to be considered accurate? The location of zmanim are calculated based on degrees of longitude (east to west) and latitude (north to south).

The earth’s circumference at the equator is about 40,000 km (about 25,000 mi). There are 360 degrees of longitude around the world (The 0° line is centered on the Royal Greenwich Observatory in England, and longitude lines extend 180° to the west and -180° to the east). For simplicity we will deal with longitude degrees at the equator. If we divide the earth’s circumference by 360°, each degree of longitude will be 111 km (69 mi) apart. The sun’s path travels 1° of longitude in 4 minutes, so calculating zmanim with one degree accuracy (no decimal points such as the latitude of 40° and longitude of -74° for Lakewood, NJ, a point in the Atlantic about 3 mi off the coast of Toms River, NJ) results in zmanim accurate to 4 minutes in each direction or an 8 minute spread, not quite accurate enough to rely on. Moving to one decimal point will pinpoint the location for zmanim calculation to an accuracy of 11 km or 48 second accuracy. That is close to being accurate enough, especially given the inaccuracy of solar time calculations resulting from hard to predict refraction caused by varying atmospheric conditions. However, this should be avoided. Adding a second decimal point (such as the latitude of 40.09° and longitude of -74.22° for Lakewood, NJ – a spot at the edge of Lake Carasaljo in Lakewood) would have a precision of about 4 seconds, more than enough accuracy for zmanim.
A concrete example of how zmanim differ from place to place in a small area would be the difference between Beth Medrash Govoha (BMG) and the Westgate Bais Medrash in Lakewood. They are 2.7 km (1.69 mi) or a drop more than 0.01° apart and calculations show that there is about a 6 second difference in sunrise and sunset times between these two locations.

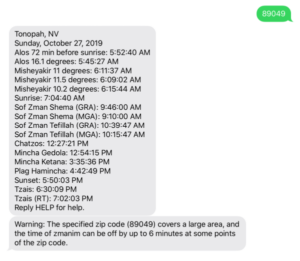
From time to time I am contacted by developers with zmanim related technical questions. Debugging their issues often requires information on the latitude and longitude that they are using to try and replicate the issue. Often the latitude and longitude are sent with multiple decimal points. The most extreme was 14 decimal points. To understand the ridiculousness of this level of precision, see the table below. To read more on the subject, see the Stack Exchange page Measuring accuracy of latitude and longitude? and the xkcd cartoon on the subject.

Decimal places	Degrees	Distance	Notes
0	1	111 km	A state or small country
1	0.1	11.1 km	City
2	0.01	1.11 km	Neighborhood
3	0.001	111 m	A specific cul-de-sac
4	0.0001	11 m	A corner of a house
5	0.00001	1.1 m	A person in a room
6	0.000001	11 cm	A small siddur
7	0.0000001	1 cm	The size of Waldo on a page
8	0.00000001	1 mm	A grain of sand
9	0.000000001	111 μm	The width of a hair
10	0.0000000001	11 μm	A grain of pollen
11	0.00000000001	1 μm	A smoke particle
12	0.000000000001	111 nm	The width of a COVID virus
13	0.0000000000001	11 nm	A red blood cell
14	0.00000000000001	1 nm	The length your nails grow every second
15	0.000000000000001	100 pm	An atom. If you need this precision, you probably belong in Lawrence Livermore

ZIP Codes and Zmanim – A Practical Approach

99557 ZIP code area (the largest in the USA)

As mentioned in the ZIP Codes and Zmanim – Use With Care article, using ZIP codes to geolocate your position for zmanim can be problematic when the zip code is large. With large zip codes, zmanim on the west side of the zip code can be quite a bit later than zmanim on the east side of the zip.

Recently, Lazer Guttman created an SMS based zmanim service at (914) 409-9394 that provides a warning when zmanim are requested for large zip codes. This approach is probably the best that can be done. I would recommend that any zmanim service that is zip code based (and does not have a map to allow zeroing in to a precise location), use this data to provide a warning whenever the zip codes is wider than 0.5° of longitude. A degree of longitude spans 4 minutes (regardless of the latitude), so half of a zip code with half of a degree would span 2 minutes (one minute east or west of the center). It should be noted that Canadian postal codes are much smaller than zip codes (usually covering one side of a city block), and most likely do not face the same issue. A spreadsheet listing all zip codes with the maximum longitude and latitude distances (in degrees), was generated by Avraham David Gelbfish from OpenDataDE that is based on US Census data. His Python source code is below.

import json
import csv

jsonfile = open("tl_2019_us_zcta510/out2.geojson")
zipcodes = json.load(jsonfile)

def getop(geolist, operation, longitude = None, latitude = None):
    if isinstance(geolist[0], list):
        answers = [getop(geo, operation) for geo in geolist]
        for answer in answers:
            lat, lng = answer
            if latitude is None:
                latitude = lat
            if longitude is None:
                longitude = lng
            latitude = operation(latitude, lat)
            longitude = operation(longitude, lng)
        return latitude, longitude
    else:
        return geolist

with open("out2.csv", "w") as csvfile:
    zwriter = csv.writer(csvfile)
    zwriter.writerow(["Zip", "Latitude max distance", "Longitude max distance"])
    for zipcode in zipcodes["features"]:
        zip = zipcode["properties"]["ZCTA5CE10"]
        geometry = zipcode["geometry"]["coordinates"]
        maxlat, maxlng = getop(geometry, lambda x, y: x if x > y else y)
        minlat, minlng = getop(geometry, lambda x, y: x if x < y else y)
        dlat = abs(maxlat - minlat)
        dlng = abs(maxlng - minlng)
        zwriter.writerow([zip, dlat, dlng])

ZIP Codes and Zmanim – Use With Care

There are many zmanim services and apps that use ZIP codes as a location finder for calculating zmanim. While very convenient, there is a potential pitfall in using ZIP codes for geolocation. In general, ZIP code geolocation services will provide the center of the ZIP code and zmanim apps calculate zmanim for that location. The issue arises with large ZIP code areas mostly found in rural areas. Take the following two extreme cases that have very large ZIP code areas. ZIP code 89049 for rural Tonopah, NV, is 195 km (121 mi) from east to west. The eastern boundary of this non-contiguous ZIP code has a longitude of -115.417°, while the western boundary is -117.625°. This means that there are 2.2° of longitude between the eastern and western borders of this ZIP code. The earth rotates 1 degree every 4 minutes, so zmanim at the eastern and western edges of this ZIP code are approximately 8.8 minutes apart. Using the typical center of the ZIP based calculations would mean that zmanim would be about 4.4 minutes different at the edges compared to the center. Moving to something a bit more extreme, is the case of ZIP code 99557 of Aniak, Alaska and its surrounding area. This ZIP code is 415 km (258 mi) from east to west. The longitude of the eastern edge of the ZIP code is -153.032°, and the western edge is -160.783°. Being farther north and therefore having shorter distances between degrees of longitude, this ZIP code stretches across 7.7° of longitude. The zmanim difference from the center to the edges of this ZIP code is 15 and a half minutes (31 minutes across the ZIP). While it is indeed rare to have such large distances, there are 193 US ZIP codes that are over 1° of longitude wide, meaning that the zmanim difference for these ZIP codes are at a minimum 4 minutes apart, or 2 minutes off from the center. There are 1,463 or 4.4% of all ZIP codes with 0.5° or greater distance between east and west (a minimum of a 2 minute zmanim difference between the east and west zide of the ZIP code). zmanim software developers should be aware of this, and take care to alert users of possible inaccuracies when using large ZIP code areas, or require addresses or more specific location information for large zip codes.
Let’s contrast the above with Lakewood, NJ. With 0.107° of longitude from east to west, zmanim are 24 seconds later on the west side (the intersection of New Central Ave & N Hope Chapel Rd) than the east side (Shinn Cranes, 1600 Ocean Ave). New York City is larger, and from the western edge of Staten Island to the edge of Glen Oaks, the eastern edge of Queens there is a 2 minute and 11 second difference in zmanim.
See the Calculation of Zmanim VS Other Sites post for additional related material.
I thank Avraham David Gelbfish for generating the ZIP code longitude range for all 33,093 ZIP codes from the US Census Bureau ZIP code shape files.