Category: Zmanim

An important aspect of calculating accurate zmanim, is ensuring that the timezone information on the computer generating the zmanim is kept up to date. The volunteer maintained IANA time zone database (also known as the tz, zoneinfo or Olson database) is used globally by computers to store time zone information. Failure to keep up to date with the latest database will result in potentially generating zmanim that can be off by an hour or more in parts of the world. This time zone database is updated multiple times a year as locations around the world change their time zone information. Often changes are to the start and end of DST in various zones, but it sometimes includes year-round changes and newly introduced time zones that have rules differing from the geographic area around them. There is a general lack of awareness by zmanim software developers and system maintainers hosting zmanim apps, of the criticality of keeping this data up to date. A lack of keeping it up to date can result in the possibility of significant issues in zmanim calculations. Subscribing to the tz announcements mailing list will keep you up to date on the latest zone changes.

Timelines for Time Zone Data Updates

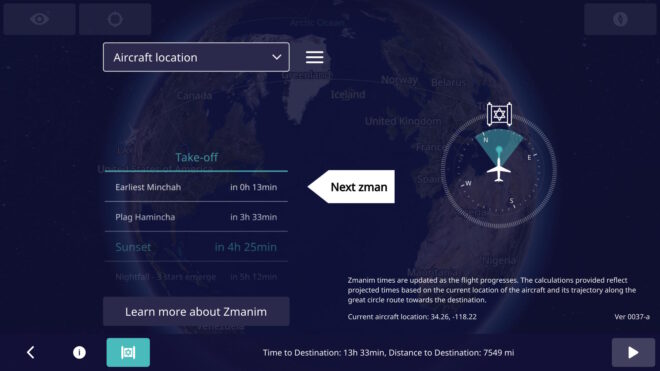
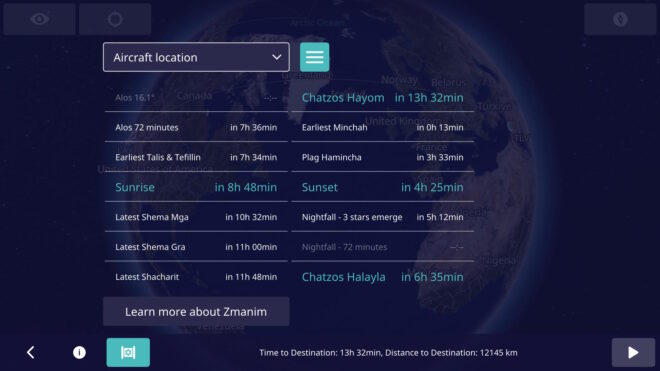
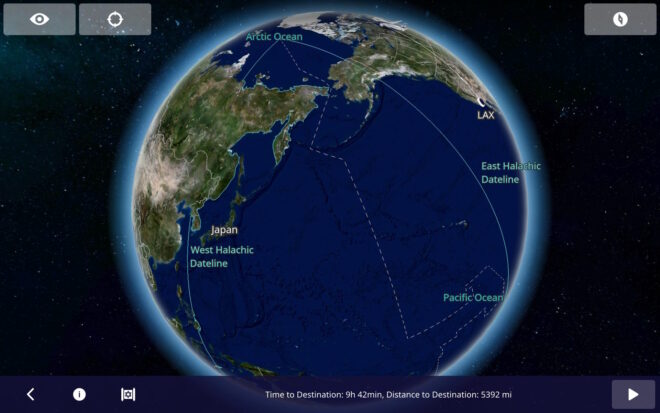
There are times when updates to the database are not released until after the changes take effect, and there are cases where the announcements are made very shortly before they take effect. An example of this was Lebanon’s 2023 change and reversal. On Mar 23, 2023 Lebanon announced that the DST that had been scheduled to start 2 days later on Mar 25 was being postponed to Apr 20. The IANA time zone database 2023b was released a day later on Mar 24 (2 days after the 2023a release). On Mar 27 they announced that they were moving to DST on Mar 29. On Mar 27, 2023c was released that restored an identical version to what had been released in 2023a.
Here is a timeline from the 2024a update for Kazakhstan (that has a small Jewish community impacted by the change). The change unified time zones for the entire country (that stretches 3,000 km /1,900 mi from east to west and geographically spans 4 time zones) from two (UTC+6 and UTC+5) to one UTC+5 zone. The timeline shows that despite being on top of things, you can’t always ensure that you are up to date.

• Oct 19, 2023 – Discussions started about a proposed change to unify Kazakhstan on a single time zone. On Nov 12, 2023 – A draft decree about the change was published.
• Dec 7, 2023 – The Kazakh Ministry of Trade and Integration announced the decree formalizing the changes.
• Jan 19, 2024 – The changes were brought to the attention of the IANA Time Zone Database maintainers. It is not unusual for a delay like this in notifying the maintainers of a change.
• Feb 1, 2024 – The time zone data change was released as 2024a.
• Feb 2, 2024 – PECL timezonedb package was released.
• Feb 4, 2024 – Moment.js‘s Moment Timezone releases v0.5.45 with the change.
• Feb 14, 2024 – Android Mainline PR is merged. It would be available to most Android 10 devices within 24 hours. Older Android versions will have to wait for the next release.
• Mar 1, 2024 – At the stroke of midnight, the clocks in part of Kazakhstan rolled back to Feb 29 at 11pm, resulting in a 25 hour leap year leap day.
• Mar 6, 2024 – Node.js code was initially updated on the main branch on Feb 15 and an issue was opened on March 1 to have a release with the updated zone information. The non-LTS version 21.7.0 with the change was released om March 6. LTS versions 20.0.12.0 and 18.20.0 with the changed were released on March 26, 26 days after it took effect.
• Mar 26, 2024 – Windows made the first update available via the March 2024 non-security preview update (that most do not install), 26 days after the change took effect.
• Apr 9, 2024 – General availability of the Windows patch was released, 40 days after it took effect.

Updating Operating Systems and Various Languages

Below are the basics for keeping your system’s time zone database up to date. Note that there are times when the announcements of changes do not give much warning, and it is not always possible to keep perfectly up to date on some platforms. If you have information on languages and systems not covered here, please post information in the comments section.

• Windows – Keep your Windows Updates up to date with optional updates. Systems set for security updates only, will never receive this update. See the information above on the windows portion of the timeline section.
• Linux – Patches are usually available immediately after the release by the IANA team. Here is some info, but be sure to read the manuals before trying things. Ubuntu you would run something like sudo apt update && sudo apt upgrade -y tzdata. For Redhat it would involve something like sudo dnf update && dnf upgrade -y tzdata.
• Android devices receive timely time zone updates for the devices current location, that will often not address issues in updating zone information for other locations. When generating zmanim for another location, care must be taken to ensure that the underlying zone database is up to date. Note that as of Android 10 (released in Sep, 2019 and currently only on about 20% of devices), the TZDB module was enhanced to update via the Mainline modules system that speeds up deployment of the updates. The Android tzdata process was enhanced late in 2023 to separate this to a standalone process that can be quickly updated multiple times a year without having to wait for other Mainline updates. Developers who want to package their own database to support older Android devices can package the Joda-Time for Android with their app, but they would have to ensure that they update their app every time a new zone database is released.
• Java provides a TZUpdater tool (download) that can can be used to update the time zone database in Java. Having the latest Java release is not reliable enough, since there are time zone changes more often than the twice yearly release (though minor versions are updated more often).
• JavaScript / TypeScript that use Moment would have to update their package.json and run npm install to receive updates. Luxon seems to use the operating system’s tzinfo. See info for Linux and Windows above. For other packages or libraries, research is needed.
• PHP out of the box only updates the zone data on new releases, They maintain the timezonedb PECL package to deal with cases (like ours) where up to date zone data is needed, but it requires regular updates.
• Python uses the operating system’s tzinfo. See info for Linux and Windows above. Alternatively, use pytz.
• Ruby uses the operating system’s tzinfo. See info for Linux and Windows above.
• Go uses the operating system’s tzinfo. A standalone copy can optionally be embedded in the Go executable.
• iOS – I was unable to find any reliable information on the subject. Apple support declined to provide any information on the subject besides confirming that they push time zone updates in a timely manner.

For many systems, cron or other jobs are needed to keep the database updated on a regular schedule. For many, a restart of the system may be required.

Warning: Inexpensive shared hosting poses significant challenges to keeping your system zone database current. There are many aspects that you have no control over, and keeping the time zone database up to date is often not high on the agenda of risk-averse shared hosts.

Additional Complexities with Mobile Devices

There is an additional set of complexities for time zones for mobile devices. While this affects Macs and possibly Windows, very few if any are using native zmanim apps on those platforms.

• One of the more common complaints about incorrect zmanim end up being caused by the device being set to the incorrect time zone. Most devices change their zone automatically, but some users manually change things and when they travel to a different zone without changing the zone, it results in incorrect zmanim. Mobile developers should explore detecting that the time zone on the device is different than the expected time zone, and alert the user to check the devices time zone setting, while ensuring that it does not have issues when there is no cellular signal (such as when flying).
• Users in Israel may find themselves in areas where the phone sets the zone to Asia/Hebron or Asia/Gaza. Those areas have different DST rules than Israel, and will cause issues when the DST rules differ. A way to handle this situation in an app is to ensure that the app detects the setting of these two zones and use Asia/Jerusalem. I am unsure if Israeli cell providers return the expected zone setting in the West Bank (or Gaza).

Here is sample java.time.ZoneId code to address the second issue.

ZoneId zi = ZoneId.of("Asia/Hebron");
if((zi.getId().equals("Asia/Gaza") || zi.getId().equals("Asia/Hebron"))){
    zi = ZoneId.of("Asia/Jerusalem");
}

Historical List of Time Zone Changes

To give an idea of the scope of time zone changes (that some assume are rare or trivial), here is a list of changes to the database. The year 2009 sticks out with 21 published changes to the database, but as you can see, there are many years numerous changes published. This list excludes technical, historical (where there are corrections to the history of time zone changes years after the fact) and some irrelevant changes. There are many examples where a location made changes more than once a year, and those are not broken out. You can see some patterns here of countries that change very often. Ramadan is a cause of many changes in Muslim countries.