 Determining zmanim times while on an airline flight is rather complex compared to calculating it for a fixed location. Some of the complexity involves:
Determining zmanim times while on an airline flight is rather complex compared to calculating it for a fixed location. Some of the complexity involves:
- Where you are currently located
- Your Speed
- Direction of travel / flightpath
The above 3 variables impact the calculation of what the zmanim are in your current location and where you will likely be when various zmanim are met.
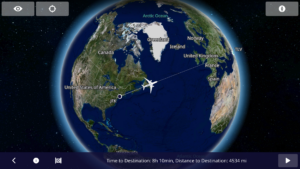
Surprisingly, the hardest part is figuring out your current location. The shortest point between 2 points on the globe is the great circle route. Though it is the shortest path, airliners rarely fly this way. To take advantage of prevailing winds such as the Gulf Stream, or to avoid bad weather, airlines often fly much longer routes and as a passenger you often do not know exactly where you are.
Yes, the airline shows you a nice location map, but getting your exact coordinates from the map is not something that they usually supply. From a practical perspective, many people on domestic and short international flights will manage to figure out davening times by themselves. As a general rule of thumb, it is time for Shacharis when the sun rises and time for Maariv when it gets dark. Please keep in mind that most poskim are of the opinion that we use zmanim at sea level elevation, or ground level, and not the 37,000 foot elevation of the flight. This elevation results in a difference of approximately 20 minutes in sunrise and sunset times. Not sure when Mincha time is? Wait until shortly before sunset. Just keep in mind that when flying due east (such as a flight from NY to Israel), you are flying in the opposite direction as the sun and the time for davening is compressed. While you may expect sof zman krias shema to be 1/4 of the way into the day, in this case the davening window is compressed into a much shorter time. The real complexity is in flights that cross the halachic dateline, polar flights and to a lesser degree, cross-Atlantic and Pacific flights. This article will not delve into the halacha of in-flight zmanim, but solely on the technical aspects of figuring out the zmanim times.
GPS
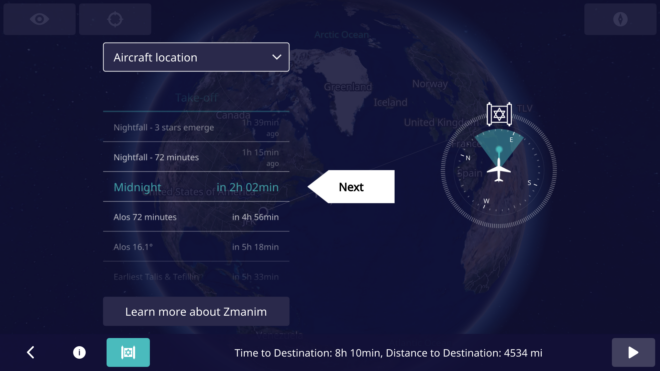
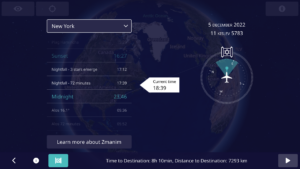
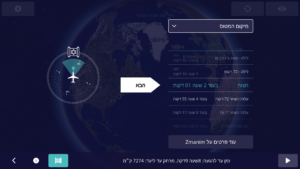
Using your phone’s GPS to identify your in-flight location, or even a standalone GPS device will usually not work once you are away from cell towers (where your GPS no longer has the assistance of A-GPS). GPS signals are very weak and your GPS receiver typically does not have an antenna strong enough to pick up the signals in an aluminum or even newer carbon fiber composite airplane like the Airbus A350 and Boeing 787. To receive a signal, an external GPS receiver is usually required and assuming that you can get a signal (it helps if the external receiver is placed by a window), we can proceed. Note that while you would expect that the CFRP body of a Boeing 787 would allow for a much stronger signal than aluminum airliners, the graphite (and probably other materials) in the 787 and A350, CFRP in conjunction with the electrochromic windows on the 787, completely block GPS signals. In addition, to protect from lightning strikes, the A350 has a metal mesh embedded in the CFRP that further reduces the signal penetrating into the aircraft body. It is this shielding as opposed to GPS jamming that blocks signals on El-Al (and other airlines) 787s and A350s. In my testing with an external GPS device designed for aviation such as the Dual XGPS 160, the composite A350 and 787 both do not allow enough GPS signal through for a GPS receiver to provide a location fix. It may be surprising that it is easier to receive the weak GPS signal in an aluminum fuselage than a composite one, but keep in mind that carbon fiber is an excellent electrical conductor. Carbon fiber was used as the filament in Thomas Edison’s early light bulbs and does not let RF signals through and effectively acts as a Faraday cage. If you are able to receive a GPS signal, you can accurately calculate zmanim for your current location using tools such as the KosherJava zmanim map. Just change the latitude and longitude to what you see in your GPS in the URL https://kosherjava.com/maps/zmanim3.html?lat=75.74&lng=-63.22&zoom=3. While not an ideal solution, it does work. The same works for the rare airlines whose maps do show accurate GPS coordinates. Please note that Wi-Fi based geolocation will not work on your flight (in my testing it gave the location of the service provider headquarters).
Precalculated Flight Paths
Another way to figure out where you are located when in the air is via a precalculated flight path. This allows programs such as the Chai Tables Chai Air Times program for Windows and Android to work. However, they just calculate a great circle route between the origination and destination locations, something that is not very accurate. Currently MyZmanim’s Inflight charts are the most practical. These charts calculate the average path of the 5 previous flights in an attempt to better estimate your flight path and provide precalculated charts based on the time you take off. Since it is just an estimate, the charts provide a relatively large window of time where zmanim may happen. This is painful and causes a lot of confusion and uncertainty, but is probably unavoidable. While this solution is currently the best that I am aware of, there are a number of issues with it. For one, much of the flight path over the oceans and Arctic that are provided by services such as FlightAware and others (that are used by MyZmanim) are just educated guesses for cross oceanic or Polar flights, since there are no ADS-B receivers in much of this area. As a matter of fact, this terrestrial ADS-B receiver-free area comprises 75% of the globe. Even if the previous flight paths were accurate, your current flight may be very different. Flights such as the Cathay Pacific flights from the NY area to Hong Kong fly either east or west depending on wind conditions. MyZmanim deals with this scenario by providing both east and west maps (based on the in-flight map you would use one or the other) and indicating the portion of a flight-path that is unknown, but this is a warning that does nothing to help you accurately calculate zmanim.
ADS-B Receivers
Every airliner broadcasts its position, heading, altitude and speed using ADS-B. A technical user can bring an ADS-B-receiver with him on the flight and use it to retrieve the current information on his flight. This would work even when there are no ground based ADS-B receivers. This is something costly and beyond the technical ability of the vast majority of flyers.
The future
Due to issues in tracking flights that came to light with the disappearance of Malaysia Airlines Flight 370, satellite based ADS-B tracking is rolling out and will be mandated. This will make it much easier for services such as MyZmanim to provide more accurate pre-flight estimates, since services such as Flight-Aware will be able to provide more exact historical flight paths. For users who do have in-flight Wi-Fi, services such as FlightAware will be able to provide almost real time location (note that many services have a 5 minute delay and are not really real-time), allowing future Wi-Fi connected zmanim apps to tap into this and provide accurate zmanim.

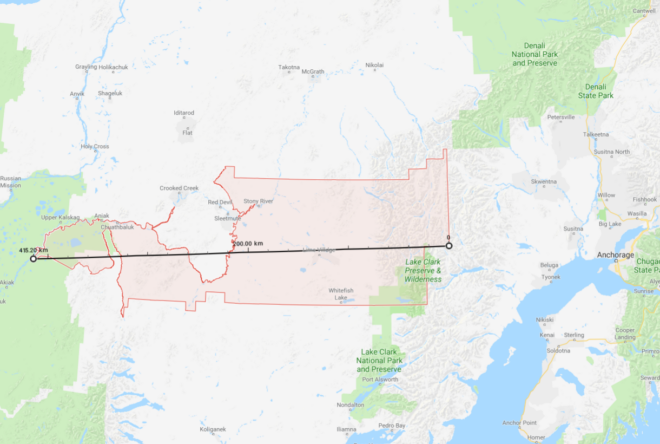
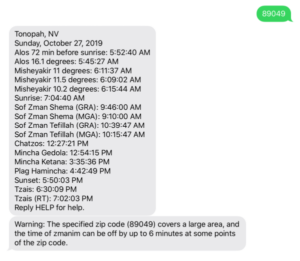
 While overly broad ZIP code based zmanim geolocation
While overly broad ZIP code based zmanim geolocation 
 Determining zmanim times while on an airline flight is rather complex compared to calculating it for a fixed location. Some of the complexity involves:
Determining zmanim times while on an airline flight is rather complex compared to calculating it for a fixed location. Some of the complexity involves: