The Yereim’s Bein Hashmashos

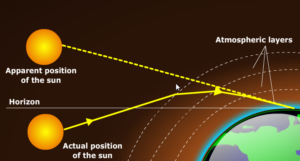
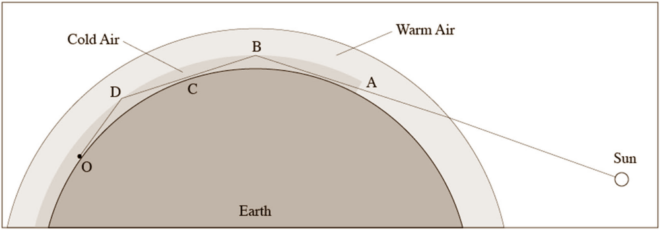
Rabbi Eliezer of Metz (known by his acronym The רא״ם Re’em), a disciple of Rabbeinu Tam, in his Sefer Yereim ספר יראים chapter 274, states that bein hashmashos starts the time it takes to walk three quarters of a mil before sunset, and ends at sunset.

פירוש משתשקע החמה דר׳ יהודה ור׳ נחמיה משמתחלת לשקוע שנוטה מעט ומכירים העולם שרוצה להכנס בעובי הרקיע … ולשון משתשקע משמע הקדמה … וכן נראה לי עיקר דמשתשקע החמה הוא קודם שקיעת החמה דעולא ולא כדברי רבינו יעקב … ואין להקפיד על צאת הככבים … אע״ף שאין הכוכבים נראים … שלילה גמור הוא כפירושי.

The Yereim’s opinion is brought down by other Rishonim including the Mordechai and Rav Alexander Suslin HaKohen in his Sefer Agudah. The Yereim is mentioned by the Bach as a reason for the minhag of starting Shabbos early. The Yereim’s times are not brought down by the poskim lehalacha.

The Time to Walk a Mil

The time to walk a mil is based on the Gemara in Pesachim 93b – 94a. The time ranges in the poskim and includes 18, 22.5 and 24 minutes. Three quarters of these mil times would be 13.5, 16.875 and 18 minutes. It should be noted that the Yereim is of the opinion that a mil is 24 minutes. The above mentioned Mordechai who quoted the Yereim is also of the same opinion. We will hopefully discuss in detail the various opinions on the time to walk a mil in a future article.

The Addition of the Yereim’s Times to the KosherJava Zmanim Library

As of the 2.1.0 release of the KosherJava zmanim library, the Yereim’s bein hashmashos times have been added to the KosherJava zmanim library/API. There are six variants of these zmanim that were added. These include the three exact minute offsets mentioned above, as well as the conversion of these three times to degrees (elevation angle, or solar zenith angle). The only prior degree based time for the Yereim that I am aware of is in Rabbi Yedidya Manet’s Zmanei Halacha Lema’aseh (זמני ההלכה למעשה מהרב ידידיה מנת). The Zmanei Halacha Lema’aseh charts calculate bein hashmashos in degrees based on the 18 minute (3/4 of a 24 minute mil, see p. 27 in the 4th ed. published in 2005), but does not clarify the degrees used. At Rabbi Yaakov Shakow’s recommendation, I used the refraction value of 31/60 or 0.516° that exists in Israel, as opposed to the global average of 0.566°. This more stringent refraction is mentioned in the Zmanei Halacha Lema’aseh (p. 11) and used in the לוח עתים לבינה Luach Itim Lebinah. I also slightly rounded the times. These small tweaks resulted in a trivial maximum 19 second chumra vs the non-rounded global average refraction. The resulting degrees of elevation angle for the Yereim’s bein hashmashos are 2.1°, 2.8° and 3.05°. Solar zenith angles are traditionally calculated using the sun’s position without adjusting for refraction and without accounting for the solar radius (i.e. it is the position of the center of the sun in a vacuum). This does not impact the calculated time, it is simply the convention used. In the upcoming 8th edition of הרב דוד יהודה בורשטין Rabbi Yehuda Burstein’s זמנים כהלכתם / Zmanim Kehilchasam he mentions that

הזמן הנ״ל של 18 דקות לפני השקיעה המישורית הוא הזמן רק במרכז א״י ביום הבינוני כנ״ל, ובכל מקום בכל יום מחשבין זאת לפי שיטת המעלות, דהיינו דבודקים כמה מעלות מעל האופק נמצאת השמש במרכז א״י ביום הבינוני 18 דקות לפני השקיעה המישורית, ואותו מספר מעלות של השמש מעל האופק בכל מקום בכל יום הוא הזמן של ״היראם״. ועוד יש להוסיף זמן ל״תוספת שבת״, ובזה יוצא ידי כל שיטות הראשונים ואשרי חלקו.

A future article will address the proper date to use for converting minute-based times to degrees below (or above) the horizon and show how to use the KosherJava Zmanim code to calculate this.
I would like to thank Rabbi Yaakov Shakow for his help and suggestions.

Sample Code

Below are code examples for all six variants of the Yereim’s Bein Hashmashos (spelled BainHashmashos in the code).

GeoLocation yerushalayim = new GeoLocation("Jerusalem, Israel", 31.778, 35.2354, 0, TimeZone.getTimeZone("Asia/Jerusalem"));
ComplexZmanimCalendar czc = new ComplexZmanimCalendar(yerushalayim);
Date bh18Min = czc.getBainHasmashosYereim18Minutes();
Date bh3Pt05Deg = czc.getBainHasmashosYereim3Point05Degrees();
Date bh16Pt875Min = czc.getBainHasmashosYereim16Point875Minutes();
Date bh2Pt8Deg = czc.getBainHasmashosYereim2Point8Degrees();
Date bh13Pt5Min = czc.getBainHasmashosYereim13Point5Minutes();
Date bh2Pt1Deg = czc.getBainHasmashosYereim2Point1Degrees();

SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd h:mm:ss a z"); //set the output format
sdf.setTimeZone(czc.getGeoLocation().getTimeZone()); //set the formatter's time zone
System.out.println("Bein Hashmashos 18 min:     " + sdf.format(bh18Min));
System.out.println("Bein Hashmashos 3.05°:      " + sdf.format(bh3Pt05Deg));
System.out.println("Bein Hashmashos 16.875 min: " + sdf.format(bh16Pt875Min));
System.out.println("Bein Hashmashos 2.8°:       " + sdf.format(bh2Pt8Deg));
System.out.println("Bein Hashmashos 13.5 min:   " + sdf.format(bh13Pt5Min));
System.out.println("Bein Hashmashos 2.1°:       " + sdf.format(bh2Pt1Deg));

The output of the above code (assuming that the calendar was set to March 16, 2020).

Bein Hashmashos 18 min:     2020-03-16 5:29:58 PM IST
Bein Hashmashos 3.05°:      2020-03-16 5:29:40 PM IST
Bein Hashmashos 16.875 min: 2020-03-16 5:31:05 PM IST
Bein Hashmashos 2.8°:       2020-03-16 5:30:51 PM IST
Bein Hashmashos 13.5 min:   2020-03-16 5:34:28 PM IST
Bein Hashmashos 2.1°:       2020-03-16 5:34:09 PM IST

FAQ: Zmanim and Leap Seconds

Leap Second

Questions:

Does the KosherJava Zmanim API account for leap seconds?
Did the magnitude 9.0-9.1 Tōhoku earthquake in Japan that changed the wobble of the earth impact zmanim calculations?

Answers:

Yes
Yes, but infinitesimally

Before delving into the answer, I would like to note that zmanim accuracy / precision down to the second that are supported by the API are really nonsense, because variations in refraction make this accuracy pointless. The second (or millisecond) zmanim accuracy / precision subject will hopefully have its own article in the future.
Since 1972, 27 leap seconds have been added to UTC time VS International Atomic Time (TAI). This is in addition to the initial 10 seconds added in 1972 to reflect pre-1972 corrections. The reason for adding leap seconds is to correct our clocks for incorrect original estimates of the speed of earth’s rotation. Assuming that you keep your clock time correct (and add the leap seconds), no change in any zmanim calculations by either the KosherJava zmanim library, or any other zmanim programs or APIs are needed. However, if you have a very accurate clock, and did not change it since 1972, your zmanim calculations will be off by 37 seconds. This is not something any zmanim APIs, apps or programs should have to deal with. Had we added any corrections for leap seconds, your zmanim calculations would be inaccurate.
As far as the Tōhoku earthquake in Japan, this is really the same question as the first question. Yes, that earthquake slowed down earth’s rotation by 1.8 microseconds or 1.8 millionth of a second (meaningless for zmanim). This as well as the impact of other earthquakes that impact earth’s rotation are factored into the leap second calculations that “correct” the time of our clocks and ensure that your zmanim are correct.

Technical Details

The leap second corrections address incorrect clock time that result from a slower earth rotation than expected. To get a drop more technical (thank you Pinny Markowitz), when the rate or the angle of rotation changes (due to earthquakes or other natural or man-made changes such as building of the Three Gorges Dam), the changes are minuscule. These small changes as well as the original incorrect calculation of the length of the day add up over time. On occasion (about every 2 years) the accumulated difference is significant enough to warrant introducing (or theoretically removing, something that has yet to happen) a leap second to reconcile our clocks with the natural one. On any given day, UTC time always considers 86,400 (60 * 60 * 24) seconds as a day. On the day with a leap second, UTC time still considers the day as having only 86,400 seconds, but a second is added to account for each of the seconds over a year or more being a drop too short. There are various ways of making system clocks conform with the UTC standard, but the net effect is always the same, an extra second is added. UTC doesn’t view a second the same way that the atomic clocks (International Atomic Time) do. UTC views a second as 1/86,400 of a relative day (that is actually 86,400.002 seconds long on average), while, atomic clocks count a day as 86,400 fixed length seconds. Fortunately, the approach of adding leap seconds is exactly what we need when calculating zmanim. By ignoring leap second events in zmanim code, and instead focusing on the measurements of a relative day, we can yield calculations that will be correct in the context of a relative day (assuming that you properly adjust your clock).

The Novaya Zemlya Effect’s Impact on Zmanim

Novaya Zemlya Effect Distorted Sun — A Distorted Sun Caused by the Novaya Zemlya Effect (Credit: Brocken Inaglory)

You may have seen disclaimers on zmanim calendars warning of up to a 2 minute inaccuracy due to weather and atmospheric conditions. Atmospheric refraction from the earth’s atmosphere, causes the sun to be visible on average about 3 minutes earlier at sunrise, and about 3 minutes later at sunset (compared to a vacuum) due to the atmosphere bending the sunlight upwards towards the viewer. The 3 minutes is only an average, and it can swing widely due to weather and atmospheric conditions. The typical variance caused by “non-average” atmospheric conditions would usually be within 2 minutes, resulting in the 2 minutes mentioned in the disclaimers. This 2 minute variance is during usual conditions, though there are conditions that would greatly increase this time.

Refraction Explained

When the sun’s rays traveling through the vacuum of space hit the earth atmosphere, they slow down and bend upwards towards the observer resulting in the sun being visible earlier (than in a vacuum) in the morning, and later at sunset.

Straw appearing to be bent due to refraction

Refraction of the sun’s rays is not a one stage refraction, but as the sun passes through increasingly dense layers of atmosphere, the amount of refraction increases with each thicker layer. This can be seen in the diagram of refraction at sunset above. The apparent position of the sun near sunset in the image (exaggerated in the image) is height of the sun as it appears to the user, though in reality the sun is below the horizon. Refraction can easily be observed by looking at a straw in a partially filled glass. The straw appears to bend (or be broken) at the point it enters the water. This is due to increased refraction in water versus air.

Complexity in Calculating Refraction

Since the amount of refraction depends on the pressure (the denser the atmosphere is, the greater the refraction), temperature (hot air is less dense and refracts less) and to a lesser degree humidity (water vapor in the air impacts the refraction) in each layer of the atmosphere, calculating refraction is complex and requires very detailed meteorological information on the current conditions in each layer of the atmosphere in the area being computed. This can’t be done accurately in advance, and even calculations for the current day require readings from weather balloons at multiple elevations for accurate measurement, something not very practical (though the BMG Lakewood vasikin minyan and likely other minyanim as well) manually adjust the hanetz hachama time each morning based on the weather). For this reason, zmanim (as well as civil sunrise and sunset) calculations usually use a global average refraction of 34′ of a degree, or 0.5666°. The global average atmospheric refraction accounts for sunrise being between 3:01 minutes earlier (during the solstice), and 2:29 minutes earlier (during the equinox) in Yerushalayim, as opposed to the value in a vacuum (the difference depends on where in the world you are, in Lakewood, NJ the range is 3:29 – 2:57). This average atmospheric refraction is not very accurate but is commonly used since it is complex to calculate local averages. More accurate refraction figures can be calculated for local and seasonal atmospheric models, and these have been shown to be accurate to within 15 seconds 90% of the time in the case of summer and winter subtropical models used in a study in Israel. See Using a Digital Terrain Model to Calculate Visual Sunrise and Sunset Times by Rabbi Chaim Keller and Dr. John K. Hall for additional details.

Inversion and the Novaya Zemlya Effect

Under usual conditions, the atmosphere gets colder at elevation, with the warmest air being closest to earth. An inversion condition is where there is a layer of cold air under a layer of warmer air. When there is an inversion over a large area (greater than 400 km), the solar rays get ducted in the lower colder air layer (see image below) and produce an extreme refraction. This is known as the Novaya Zemlya effect and produces a solar mirage resulting in the somewhat visually distorted sun being visible much earlier than expected (see top image).

While typically a phenomena in the polar regions, a study by the University of Calgary showed that refraction can have a significant affect on zmanim even in non-polar areas. In the 2003 study (Variability in the Astronomical Refraction of the Rising and Setting Sun), they observed that the sunrise on January 10, 1991 appeared almost 12 minutes earlier than expected. The paper mentions:

On rare occasions, the Sun appeared to rise much earlier or set much later than predicted by such publications as the Tables of Sunrise, Sunset, and Twilight (USNO 1962). In our study, the sunrise of 1991 January 10 was almost 12 minutes early. This phenomenon is known as the Novaya Zemlya solar mirage (Lehn 1979). It appears to be caused by a geographically extensive temperature inversion within the boundary layer of the atmosphere. The resulting vertical density profile causes the sunlight to be ducted around the curvature of the Earth. For the purpose of this study, we defined anomalously large astronomical refraction to be an event with refraction greater than 1°. A total of 12 anomalous events were recorded (2.9%).

While these typically occur in cold areas, they can happen in other areas as well. The study authors mention that

The majority of the anomalous events took place in the cold months. Nine of the 12 events occurred between November 1 and April 30, with January having five events. At the time of the events, the average surface temperature was -10.9°C, and all events occurred with surface-inversion conditions. Surface inversions tend to form with overnight surface radiative cooling through a dry atmosphere. Typically, they persist into the early morning, even after sunrise. Even though most of the events took place in the cold parts of the year, the data suggest that the Novaya Zemlya solar mirage may not be an exclusively cold-weather or polar phenomenon. Four of the events occurred with a surface temperature greater than 0°C. One event took place 2 days after the summer solstice.

Refraction at Sunrise VS Sunset

The University of Calgary study found that extreme refraction is an order of magnitude more common at sunrise than sunset. The reason for the difference between sunrise and sunset is that

This may be because the lower atmosphere is better mixed during the day as a result of solar heating leading to a dry adiabatic lapse rate in the boundary layer. Anomalously large astronomical refraction events the “Novaya Zemlya solar mirage” occurred about 3% of the time and were an order of magnitude more common at sunrise than sunset.

That said, The Novaya Zemlya effect does occur at sunset and in warm climates as seen in this video of sunset in San Francisco. Sadly, the video does not include information on how long it delayed sunset.

Halacha

Halachically sunrise and sunset times depend on when we can see the sun, and not when it is at the horizon. As mentioned above, the average global refraction of 34′ results in sunrise appearing about 3 minutes earlier and sunset 3 minutes later than in a vacuum, and this refraction (or other similar refraction values) is what is used in all calendars (both halachic and civil). The fact that there is such potential for variation in weather conditions, and that the global average is likely not what is present where the zmanim are being calculated, is the reason that many luchos (zmanim calendars) have disclaimers about accuracy. Many calendars round off their zmanim without showing seconds due to the inability to accurately calculate zmanim because of refraction variations. Lahalacha the impact of earlier or later sunrise is limited to vasikin minyanim. A separate article may be needed to actually discuss sof zman krias shema and other zmanim‘s relation to sunrise and sunset VS the actual position of the sun in the sky (1/4 of the way across its path for sof zman krias shema). The halachic impact of refraction at sunset is much greater since it impacts the day/night boundary, but those are much rarer.
Now to the big question, does extreme refraction such as the Novaya Zemlya effect impact zmanim? The fact that it rarely impacts sunset, means that it almost academic since predicting the inversion before a vasikin minyan starts is impractical. In a conversation with one posek a number of years ago, he felt that the Novaya Zemlya Effect should not impact zmanim lahalacha due to the fact that unusual occurrences should not be factored in, and because the distorted sun is not considered the sun as far as zmanim. I would appreciate being notified if anyone receives a psak halacha on this question.