
Question:
Is there a difference in time between the zmanim of chatzos hayom and chatzos halayla (astronomical midnight and astronomical high noon / midday) besides the obvious 12 hour difference?
Answer:
I was recently asked by a developer why the KosherJava zmanim library does not have distinct calculations for chatzos halayla. The answer is that the zmanim API does indeed have the getSolarMidnight() calculation, but for the most part there is no real need for it. The time of chatzos halayla / midnight or chatzos hayom (solar transit / solar noon or midday) stays pretty constant from day to day. In the worst case scenario (on around December 22nd), the length of the solar day would increase by about 30.16 seconds from one day to the next. This does not change by location, but is the same anywhere in the world. This would mean that chatzos halayla could be a maximum of 15.08 seconds different than just using midday + 12 hours. This is something that should not really impact people. In addition, the developer in question does not even show seconds, making this a moot point. In short, chatzos on any given day should be considered accurate enough for both chatzos hayom and chatzos halayla of that day. It should be noted that the Mishnah Berurah quoting a number of achronim and the Shulchan Aruch Harav are of the opinion that chatzos halayla is exactly 12 hours after chatzos hayom. The Mishnah Berurah states in הלכות הנהגת אדם בבקר א׳ ט׳
וזמן חצות הוא תמיד באמצעות הלילה ממש בכל מקום ואפילו בלילות הארוכות או הקצרות והיא י״ב שעות אחר חצי היום …
and the Shulchan Aruch Harav in הלכות השכמת הבוקר א׳ ח׳ states that
וזמן חצות לילה הוא שוה בקיץ ובחורף לעולם י״ב שעות אחר חצי היום שהוא אמצע הלילה ממש …
Chatzos Halayla on the Seder Night
 The time of year that the zman of chatzos has the greatest impact is during the Pesach seder when people want to finish the afikoman before chatzos. During this time of the year the solar days are shrinking slightly from day to day, resulting in chatzos halayla being slightly earlier than chatzos hayom + 12 hours. The difference in the length of the solar day from solar noon on erev Pesach to solar noon on the first day of Pesach ranges from 11 to 18 seconds depending on the year. On the very late erev Pesach on April 24 that last occurred in 1929 and 1967 and will next occur in 2043 and 2062 there is an 11 second difference. On the extremely early erev Pesach of March 25 that occurred in 1899 and 2013 and will occur next in 2089 (see Rabbi Dovid Heber’s Why is This Pesach the Earliest Since 1899?) there is an 18 second difference. This 5.5 to 9 second difference in the time of chatzos hayom VS chatzos halayla on erev Pesach is something that has almost no real world impact. It is interesting to note that based on the fact that the average Jewish year is slightly longer than the average solar year, the early March 25 erev Pesach will never happen again after 2089.
The time of year that the zman of chatzos has the greatest impact is during the Pesach seder when people want to finish the afikoman before chatzos. During this time of the year the solar days are shrinking slightly from day to day, resulting in chatzos halayla being slightly earlier than chatzos hayom + 12 hours. The difference in the length of the solar day from solar noon on erev Pesach to solar noon on the first day of Pesach ranges from 11 to 18 seconds depending on the year. On the very late erev Pesach on April 24 that last occurred in 1929 and 1967 and will next occur in 2043 and 2062 there is an 11 second difference. On the extremely early erev Pesach of March 25 that occurred in 1899 and 2013 and will occur next in 2089 (see Rabbi Dovid Heber’s Why is This Pesach the Earliest Since 1899?) there is an 18 second difference. This 5.5 to 9 second difference in the time of chatzos hayom VS chatzos halayla on erev Pesach is something that has almost no real world impact. It is interesting to note that based on the fact that the average Jewish year is slightly longer than the average solar year, the early March 25 erev Pesach will never happen again after 2089.
Equation of Time (EoT)
You may have expected that the longest day of the year – the summer solstice (June 20 or 21 depending on the year) would be the day with the earliest sunrise / netz (or hanetz) and latest sunset / shkiah (and therefore the day with the latest start of Shabbos). However the earliest sunrise actually occurs on or about June 14 (at latitude 40° – it varies slightly based on latitude), a week before the longest day, and the latest sunset occurs on or about June 28, a week after the summer solstice. As mentioned above, the length of the day that we know to be exactly 24 hours on a clock is actually only an average over the year. The length of the day varies slightly from day to day. This length of day range is from a minimum of 23 hours, 59 minutes and 38.64 seconds around September 17 to a maximum of 24 hours and 30.16 seconds around December 22 vs the previous day. This accumulated length of the day difference is known as the equation of time. While the day starts shortening after the solstice, chatzos (and by extension the entire day) is moving slightly forward as the solar day (midday to midday) grows at this time of the year, resulting in the day ending later despite it being shorter.
The cause of the change is due to the following two main factors. The very minor impact of nutations (such as the Chandler wobble), axial precession and other factors are too small to make a practical difference in the EoT calculations.
The tilt of the Earth’s Rotational Axis
The tilt of the Earth’s rotational axis (also known as the axial tilt or the obliquity of the ecliptic) as compared to the plane of its orbit around the sun is one factor that impacts the length of the solar day. To understand this, note that the earth rotates on it’s axis in 23 hours 56 minutes and 4.1 seconds in relation to the stars. This is called a sidereal day. The remaining 3 minutes and 55.9 seconds or about 0.98° of rotation must be made up every earth day. Due to the 23.44° axial tilt, this 3 minutes and 55.9 seconds is only an average. 

The elliptical orbit of the earth
The elliptical orbit of the earth (or the eccentricity of the Earth’s orbit) is the second factor that impacts the length of the day. The earth’s orbit around the sun is an ellipse and not a perfect circle. Following Kepler’s second law, the earth moves slightly faster in orbit when it is closer to the sun, and slower when it is farther away. During the perihelion (it ranges between January 2 and 6 depending on the year) when the earth is closest to the sun at 91,402,500 mi / 147,098,070 km distance, it travels at 30.287 km/s, while at the aphelion (between July 3 and 7) when it is 94,509,100 mi / 152,097,700 km away, it travels at 29.291 km/s. In addition, the angular velocity of the sun is faster (in relation to the stars) when it is closer to earth. Despite it being somewhat counter-intuitive, the sun is closer to earth in middle of the northern hemisphere’s winter than during the summer. This non-uniform orbital speed impacts the length of the solar day.
The Accumulated Difference
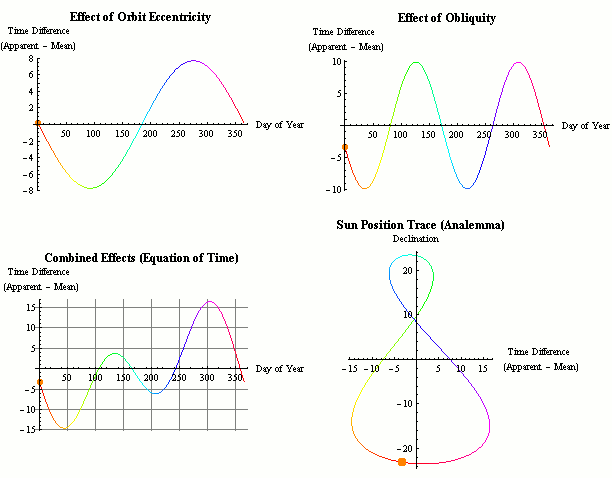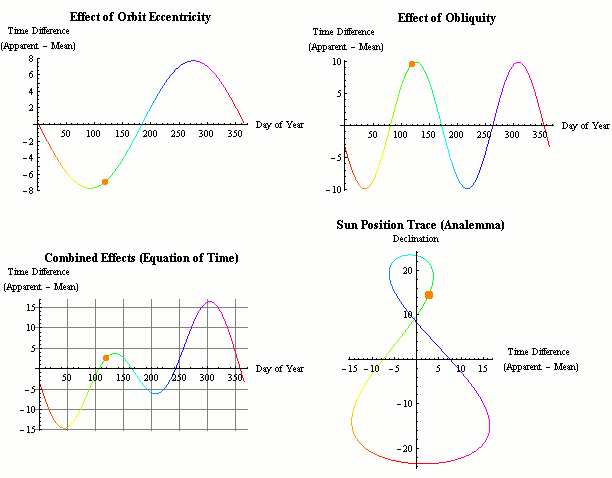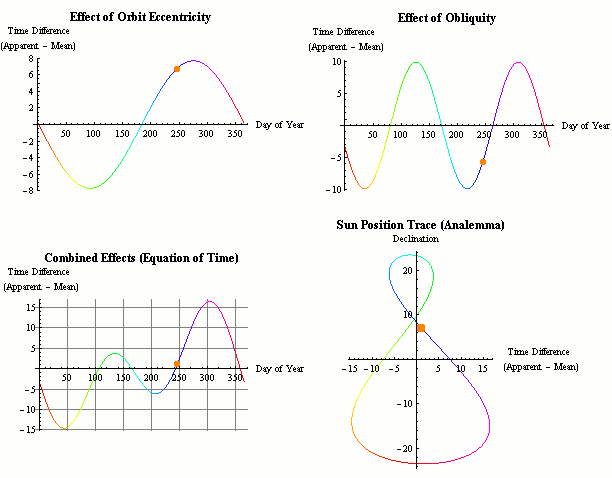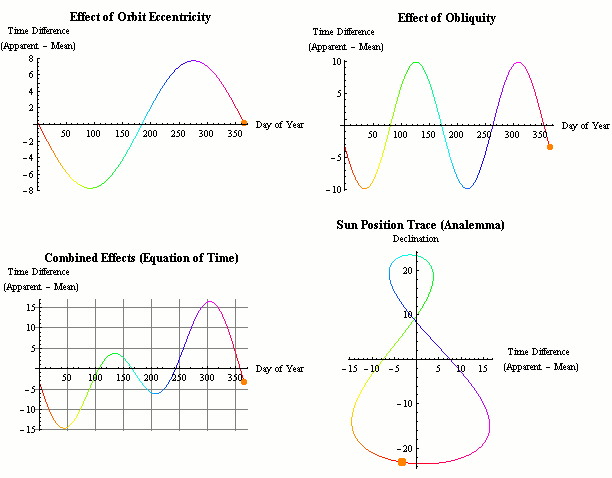 This difference between our standard clock time and the time that would be based on the exact position of the sun in the sky accumulates and is referred to as the equation of time (EoT). Equation in this case refers to equality and not a mathematical equation (though the calculations certainly involve mathematical equations), and adding or subtracting this time allows us to sync solar time and clock time (mean solar time / universal time).
This difference between our standard clock time and the time that would be based on the exact position of the sun in the sky accumulates and is referred to as the equation of time (EoT). Equation in this case refers to equality and not a mathematical equation (though the calculations certainly involve mathematical equations), and adding or subtracting this time allows us to sync solar time and clock time (mean solar time / universal time).
Please see the references section below for links that cover the topic in detail.
Thank you.
References
- Sundials on the Internet’s The Equation of Time article.
- The US Naval Observatory’s article Sunrise and Sunset Times Near the Solstices.
- The US Naval Observatory’s article The Equation of Time.
- Wikipedia’s equation of time (EoT) article.
- A video about the equation of time by ScienceOnline.
- Ask Ethan: When Is The Earliest Sunrise And Latest Sunset Of The Year?
- Forbes’ Today Is Not 24 Hours Long.
- In-the-Sky’s Equation of Time article.
I would like to thank my son Shai for the detailed work on the technical part of this article.
The calculations of EoT would presumably be the same according to the geocentric model, just with a different frame of reference and with some other changes to the orbital mechanics. If this article were to be rewritten according to that model, the heading “The Tilt of the Earth’s Rotational Axis” would be replaced with “The Tilt of the Sun’s Orbital Axis,” and the following text would be changed to match; and “The elliptical orbit of the earth” would instead be “The eccentric orbit of the sun,” again with the appropriate following changes.
The details:
In the classical geocentric approach, the various irregularities in orbits are explained by (a) the sphere (orbit) being circular but eccentric relative to the earth, and (b) epicycles. The diurnal rotation of the heavenly bodies, in that model, results from an outer sphere (the Rambam calls it גלגל היומי) that rotates every 24 hours, and forces all the others to rotate with it.
In Hilchos Kiddush Hachodesh the Rambam describes the sun’s orbit using just an eccentric circular orbit, without an epicycle. (The moon’s, he says, requires an epicycle plus several other adjustments.) Whether he held that the sun actually has an epicycle, I don’t know; as he says in chapter 11 there, he’s not aiming at perfect astronomical accuracy, just at an approximation good enough for determining the moon’s visibility on the night of Rosh Chodesh. (And in Hilchos Yesodei Hatorah, where he presents an overview of the geocentric model, he gives a total number of cycles and epicycles for all the planets, but then in Moreh Nevuchim he says that those are just the ones known so far, and there may be more.)
In his calculations, he seems to account for only two kinds of variations in the sun’s angular rate relative to earth: orbital eccentricity and precession. So his algorithm for calculating the sun’s position is: (a) from a known epoch, add the daily average angular rate of the sun in its orbit; (b) from a known epoch, add the daily average angular rate of the point of aphelion (in that system it would be called apogee); (c) subtract (b) from (a) to get the sun’s anomaly; (d) based on (c), find and apply the appropriate correction factor (equation of the center). He doesn’t seem to deal with the seasonal variations due to obliquity; I suppose that’s because he’s not giving formulas for determining the clock times of zmanim, and because throughout most of Hilchos Kiddush Hachodesh he’s using ecliptic coordinates rather than equatorial ones. (Also, he states that the sun’s orbit is tilted relative to the equator by 23.5 degrees, but doesn’t say whether he knew this tilt to gradually change over time.)
(In an e-mail exchange, R’ Hershfeld also mentioned a point his son made: that with circular orbits you can use trigonometry for calculating angular velocities and positions, whereas elliptical orbits would require calculus, which hadn’t even been invented yet in the Rambam’s time. That opens up the possibility that the Rambam would indeed hold that the orbits are actually elliptical, but chose to use circular orbits for simplicity’s sake.)
In your article about the need for summer/winter sun to travel 1.09 equitorial degrees for each 1 degree of ecliptic travel, you say 1 degree of travel to the WEST. I believe you need to change that to “east”, because that’s the direction the sun goes.
Thank you Shmuel. You are indeed correct. The mistake happened due to the fact that sky maps have east/west inverted. The article has been corrected. In addition to this correction, the seasons were also corrected.